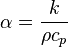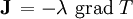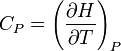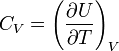熱の拡散
温度拡散率
温度拡散率(おんどかくさんりつ)は定常状態の温度勾配などをもとめるのに用いる係数である。
温度拡散率
k :熱伝導率(Js-1m-1K-1)
ρ:密度(kg m-3)
Cp:比熱容量(J kg-1K-1)
でもとめる。単位はm²/sである。
熱拡散率 (thermal diffusivity)、温度伝導率 (temperature conductivity) ともよばれる。熱拡散係数(thermal diffusion coefficient)と熱拡散率は全く異なった物理現象を表す量である。互いに異なった物質間熱の移動を説明する物理量として,相手側の物質から「熱を奪い取る能力、または熱を迅速に受け入れる容量」といった意味あいの熱浸透率と呼ばれる量がある。
熱伝導率
熱伝導率(ねつでんどうりつ、Thermal conductivity)は、熱伝導度ともいい、熱伝導において、熱流束密度(単位時間に単位面積を通過する熱エネルギー)を温度勾配で割った物理量。その逆数を熱抵抗率(ねつていこうりつ)という。
熱流束密度をJ、温度をT、温度勾配を gradTとすると、熱伝導率λとの関係は次のように表される。
熱伝導率のSI単位はW/(m・K)であり、W/(cm・K)も使われる。
熱伝導率は媒質中により温度勾配がある場合にその勾配に沿って運ばれる熱流束の大きさを規定する量であり,熱拡散率は温度勾配により運ばれる温度(熱エネルギー)の拡散係数を意味する。ここで,熱拡散係数と熱拡散率は物理的に異なった量を意味するので注意が必要である。 熱拡散係数は,混合物に温度勾配がある場合に,熱拡散により濃度勾配が生じる時の大きさを規定する物理量である。 熱伝導率=熱拡散率x定圧比熱容量x密度 である。(なお,比熱容量x密度は単位体積当たりの熱容量で,体積熱容量と呼ぶ)
また、熱伝導率が一つの物質内での熱の伝わり易さを表す値に対し、物質間の熱の伝わり易さを表す値として熱伝達係数がある。
密度
密度(みつど)は、単位体積あたりの質量である。
より厳密には、ある量(物理量など)が、空間(3 次元)あるいは面上(2 次元)、線上(1 次元)に分布していたとして、これら空間、面、線の微小部分上に存在する当該量と、それぞれ対応する体積、面積、長さに対する比のことを(それぞれ、体積密度、面密度、線密度と言う)言う。微小部分は通常、単位体積、単位面積、単位長さ当たりに相当する場合が多い。 勿論、4 次元以上の仮想的な場合でも、この関係は成立し、密度を定義することができる。
その他の密度としては、状態密度、電荷密度、磁束密度、電流密度、数密度など様々な量(物理量)に対応する密度が存在する(あるいは定義できる)。物理量以外でも人口密度や確率密度などの値が様々なところで用いられている。
密度の単位
単位体積あたりの質量としての密度は国際単位系 (SI) では キログラム毎立方メートル(kg/m3)を単位として使用する。他にも g/cm3 = kg/L などがある。
1 kg/m3 = 1,000 g/1,000,000 cm3 = 0.001 g/cm3 = 0.001 kg/L
いろいろな物の密度
(単位: g/cm3 = 103kg/m3)
* オスミウム – 22.57
* イリジウム – 22.42
* 白金 – 21.4
* 金 – 19.3
* タングステン – 19.3
* ウラン – 18.7
* 水銀 – 13.5
* 鉛 – 11.3
* 銀 – 10.5
* 銅 – 8.92
* 鉄 – 7.87
* チタン – 4.54
* アルミ – 2.70
* ケイ素 – 2.33
* マグネシウム – 1.74
* ナトリウム – 0.971
* カリウム – 0.862
* リチウム – 0.534
比熱容量
熱力学と比熱
熱力学では1モルの物質の熱容量、モル熱容量(単位はJ mol−1K−1)を用いることが多い。モル熱容量は分子熱とも呼ばれる。単位質量あたりの熱容量(比熱容量)にモル質量(単位はkg mol−1)を掛ければ、モル熱容量になる。たとえば25℃の水 (液体)ではCp = 75.291 J mol−1K−1である。
圧力一定の条件下で測定した場合は定圧比熱(記号:Cp)、体積一定の条件下で測定した場合は定積比熱(記号:Cv)と呼ばれる。
定圧比熱
定圧比熱(ていあつひねつ)とは、圧力一定の条件下で単位量あたりの物質を単位温度変化させるのに必要な熱量。
一般的記号は、CPで表し、エンタルピーの変化量の傾きを表す。
定積比熱
定積比熱(ていせきひねつ)とは、体積一定の条件下で単位量あたりの物質を単位温度変化させるのに必要な熱量。
一般的記号は、 CVで、内部エネルギーの変化量の傾きを表す。
性質
通常、液体、固体における比熱は、温度により極端に変化しないが、気体においては、エンタルピーの変化量や体積変化が大きく状態量として定圧比熱や定積比熱を考えなければならない。
理想気体においては
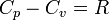
- R:気体定数
であり常にCp>Cvという関係がある(記事比熱比に詳しい)。このことを理解するために、エネルギーの出入りQについて定積の場合と定圧の場合を考えてみよう。
定積の場合、変化に際して系は仕事をしないから系に入ってきたエネルギーはすべて温度上昇に使える。ところが、定圧の場合には系の温度を上げた上で、さらに体積変化分の仕事をしなければならない。この仕事に内部エネルギーは使えない(理想気体の場合温度は内部エネルギーの関数である)から、結局この分のエネルギーも余分に外から与えてやらなければ成らないのである。
固体・液体の熱膨張は物質の混合等によるものも含め相により正にも負にもなるので両者の大小関係は不定である。
(気体の混合物については、一般的には、モル分圧比が成り立つ)
ある温度以上の単体の固体では定積モル熱容量Cvが一定になるというデュロン=プティの法則(Dulong-Petit)がある。
容積比熱
熱容量を考慮するときに、質量単位でなく体積単位の方が便利な場合があり、その場合は、容積比熱もしくは体積比熱が用いられる。単位は例えば、J/(m3·K)である。
使われる分野としては以下がある。
- 建築分野での壁材の断熱特性。用語として容積比熱がよく用いられる。
- 土壌分野での土の熱特性。用語として体積比熱がよく用いられる。
提供: フリー百科事典『ウィキペディア(Wikipedia)』